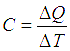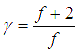Heat capacity of a system can be defined as the quantum of heat required to increase the temperature of the system by unity.
Specific heat is a property of the material. For a given material, specific heat is defined as the quantum of heat required to increase the temperature by unity, per unit mass of the material.
Specific heat at constant volume (CV,m) is the change in internal energy per unit mass of the substance, per unit temperature rise. This relates to the heat absorbed by the system for unit temperature rise, when the volume of the system remains unchanged.
Specific heat at constant pressure (CP,m) is the change in internal energy per unit mass of the substance, per unit temperature rise. This heat capacity relates to the heat absorbed by the system for unit temperature rise, when the system pressure remains constant.
Molar heat capacities CP and CV can be defined in the same fashion, as the heat required per mole of the substance to increase the temperature by unity under constant pressure and constant temperature respectively. For an ideal gas, the relation between the molar heat capacities can be given by the following equation,
CP - CV = R (universal gas constant) ….. For an Ideal Gas
The general relation between molar heat capacities for any fluid is given by the following equation.
where, α = coefficient of thermal expansion
β = isothermal compressibility
The ratio of CP to CV (CP/CV) for a gas is known as the specific heat ratio or adiabatic index and usually denoted by the Greek letter gamma (![]() ). For an ideal monoatomic gas (e.g. Helium, Argon etc), the adiabatic index is 5/3 or 1.67.
). For an ideal monoatomic gas (e.g. Helium, Argon etc), the adiabatic index is 5/3 or 1.67.
For monoatomic gases, CV = 3R/2 and CP = 5R/2 (where R is universal gas constant).
For diatomic gases which occur more frequently in natural environment and which can be considered to exhibit ideal behavior at standard conditions, CV = 5R/2 and CP = 7R/2 (where R is universal gas constant).
Thus for naturally occurring diatomic gases at near standard conditions, the adiabatic index can be approximately considered to be around 7/5 or 1.4.
The specific heat ratio or adiabatic index is related to the degrees of freedom (![]() ) of a gas molecule by the equation,
) of a gas molecule by the equation,
Monoatomic gas molecules possess only 3 translational degrees of freedom, while diatomic gases possess 3 translational and 2 rotational degrees of freedom at near standard conditions. As the temperature increases for a gas thus increasing the degrees of freedom of gas molecules in rotational and vibrational dimensions, the specific heat ratio decreases for the same molecule.