Mass balance is a fundamental concept in physics and engineering that refers to the accounting of mass in a system. It involves analyzing the flow of matter into and out of a system, as well as the storage of matter within the system. In simple terms, mass balance states that the amount of mass entering a system must equal the amount of mass leaving the system, plus any changes in the amount of mass stored within the system.
Index
1. Generalized Equation
2. Mass Balance For Chemical Reaction System
3. Mass Balance For Steady State System
4. Using The Mass Balance Equation
In essence, the principle of mass balance is based on the conservation of mass, which states that the total amount of mass in a closed system is constant over time. This principle is also known as the law of conservation of mass, and it is a fundamental principle in physics and chemistry.
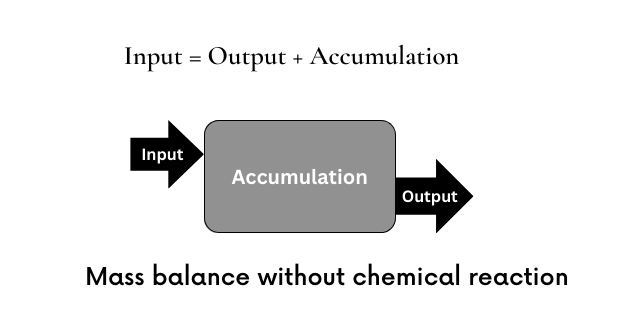
Generalized Equation
The mass balance equation forms basis to a number of process engineering calculations. Mass balance equation simply states that total mass in any system is always conserved. That is,
Total mass in = Total mass out + Total mass accumulated in the system
The mass balance can be performed for different components of the inlet and outlet streams.
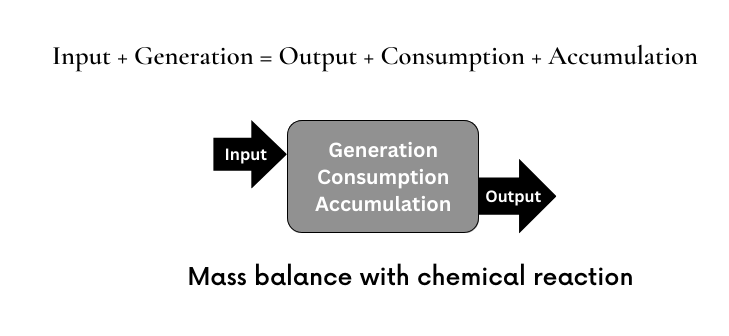
Mass Balance For Chemical Reaction System
When considering individual component instead of the total mass of a stream, it has to be kept in mind that for a reacting system, one or more components can be converted to one or more different components. Hence for individual component mass balance for a reacting system, we get a generation term and a consumption term.
The basic mass balance for a reacting system becomes,
MN in + MN generation = MN out + MN consumption + MN accumulation
M indicates mass and subscript N is second equation denotes the Nth component of the system. Hence for a system comprised N components, there are N such mass balance equations.
When equation is differentiated with respect to time, we get a mass balance equation in terms of rates. Let F denote mass flowrate, let R denote reaction rate to generate or consume a component and let A denote accumulation rate.
FN in + RN generation = FN out + RN consumption + AN
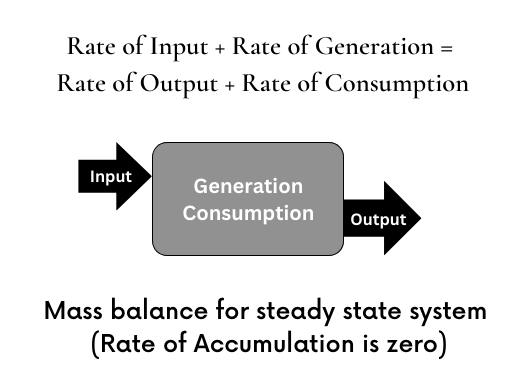
Mass Balance For Steady State System
For steady state systems accumulation rate is zero.
The mass balance equation for steady state system is,
FN in + RN generation = FN out + RN consumption
The equations presented here are very basic mass balance equations. For specific systems each term in these equations can be detailed and solved for compositions and component mass flows in the inlet and outlet streams as well as in the system under consideration.
The principle of mass balance is applied in various fields, such as environmental engineering, chemical engineering, and materials science. For example, in environmental engineering, mass balance is used to assess the flow of pollutants through a water or air system, while in chemical engineering, it is used to optimize chemical reactions by controlling the amounts of reactants and products in a system.
Using The Mass Balance Equation
The Mass Balance Equation is widely applied in many fields, including:
- Chemical Engineering: Used to track the flow of substances in chemical processes.
- Environmental Science: Applied to assess the movement of pollutants and nutrients in ecosystems.
- Economics: Used in economic models to understand resource allocation and production.
- Food Industry: Applied to monitor the production and distribution of food products.
- Pharmaceuticals: Used to track the synthesis and distribution of pharmaceuticals.