Fluid viscosity is an important fluid property in fluid dynamics. Fluid viscosity represents the frictional resistance within the fluid to shearing force acting on the fluid.
Dynamic Viscosity (Absolute Viscosity)
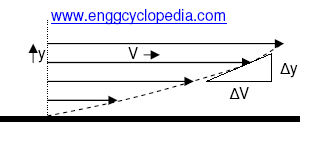
Dynamic viscosity or Absolute viscosity is used to determine the absolute viscous force resisting the fluid flow. Newton's law has established the relation between viscous force resisting the onset of fluid flow and velocity gradient in the fluid. As per Newton's law, magnitude of the viscous force which resists the fluid motion is directly proportional to the velocity gradient at the point under consideration and direction of the viscous force is opposite to the fluid flow. Consider the following figure showing the fluid velocity profile close to a stationary wall. The velocity gradient at any given point in is represented by the slope of the velocity profile curve shown in the figure.
Velocity Gradient = dV/dy ≈ ΔV/Δy (as Δy→0)
As per Newton's law,
Viscous stress = τ = - µ(dV/dy)
Here, the negative sign indicates direction opposite to the fluid flow and µ is the absolute viscosity or dynamic viscosity of the fluid which acts as a proportionality constant. Newton's law stands for viscous force per unit area of the fluid, which is represented by viscous stress. Unit of viscous stress are same as units of pressure.
Kinematic Viscosity
In some cases the ratio of viscous forces and inertial forces in a fluid flow is considered to be important. Viscous forces are represented by a density of the fluid and viscous forces are represented by the absolute or dynamic viscosity of the fluid. Hence the ratio of viscous forces to inertial forces in the fluid is represented by (absolute viscosity / density). This ratio is known as kinematic viscosity (ν) of a fluid.
Kinematic Viscosity = ν = µ/ρ
It should be noted that absolute viscosity (µ) and density (ρ) are both fluid properties dependent only of the state of the fluid (pressure and temperature). Hence kinematic viscosity of a fluid is also dependent only in the state of the fluid and not the flowrate.
Variation of absolute viscosities with fluid temperature
Absolute liquid and vapor viscosities are strong functions of liquid temperatures. EnggCyclopedia's viscosity calculators for Liquids and Vapors can be used to quickly determine the viscosity at a given temperature.
For compressible fluids (gases) the densities depend on pressure of the system and hence kinematic viscosities of gases are also dependent on pressure. For incompressible liquids, the densities are independent of pressure and hence kinematic viscosities for incompressible liquids only depend on temperature.