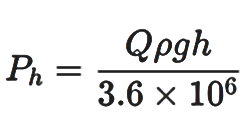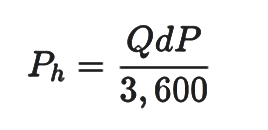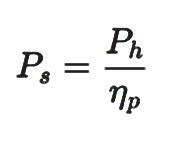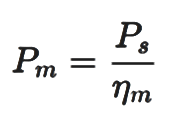Pump power refers to the amount of energy required by a pump to move a fluid through a system. Understanding power calculations are essential in various industries and applications, as it determines the efficiency and effectiveness of the pumping system. Properly sizing a pump and selecting the appropriate power source can help pumps to operate efficiently with minimum energy consumption and maintenance costs.
Table of content:
What is pump power?
Pump power equation
Pump power calculation
What is pump power?
Pump power refers to the amount of energy required by a pump to move a fluid through a system. It is typically measured in watts, horsepower, or kilowatts.
Shaft power of pump
The input power is the mechanical power in kilowatts (kW) or watts (W) that is taken by the shaft or coupling. This input power is also called Break Horse Power (BHP) or Pump Shaft Power. Shaft power is the power that is supplied by the motor to the pump shaft.
The shaft power is the sum of the hydraulic power, which is the energy imparted to the fluid being pumped to increase its velocity and pressure, and the power loss due to inefficiencies in power transmission from the shaft to the fluid. The power of a pump can be measured using a power meter or a wattmeter, which measures the electrical power input to the pump.
Hydraulic power of pump
The output power is called Water Horse Power (WHP) or Hydraulic Power. Hydraulic power of pump is the energy that is transferred from a pump to the fluid being pumped to increase its velocity and pressure. This is the useful work delivered by the pump. The mechanical power output of the pump can be measured using a torque meter and a speedometer.
Motor power
Motor power is the amount of power that is consumed by the pump motor to turn the pump shaft. It represents the electrical power input to the motor and takes into account all the losses due to inefficiencies in converting electrical energy into kinetic energy.
Pump power equation
Hydraulic power: The hydraulic power can be calculated using one of the formula below, depending on the available data.
Where, Ph = Hydraulic power (kW)
Q = Flow rate (m3 / hr)
ρ = Density of liquid (kg / m3 )
g = Gravitational constant (m / s2 )
h = height of liquid level (m)
Where, Q = Flow rate (m3 / hr)
dP = Pressure difference (kPa )
Shaft power: Shaft power is typically calculated as the hydraulic power of the pump divided by the pump efficiency as follows.
Where, Ps = Shaft power (kW)
Ph = Hydraulic power (kW)
np = Efficiency of pump
Motor power:
Where, Ps = Shaft power (kW)
Pm = Motor power (kW)
np = Efficiency of motor
Pump power calculation
Problem statement:
Calculate the pump power and motor power requirement to pump 200,000 kg/hr of water available at 250C and atmospheric pressure from a storage tank. The rated differential head requirement is 30 m.
Assume the mechanical efficiency of the pump to be 70%.
Assume the motor efficiency to be 90%.
Solution:
First we will calculate the theoretical power requirement using the pump power equation. This is the power required by the pump and provided by the motor. Next, we will divide this power requirement by the efficiency of the motor to calculate power required by the motor.
Let's go step by step through these pump power calculations.
Step1: The first step is to determine the important physical properties of water at given conditions. The only important physical property for solving this problem is the mass density of water.
Using EnggCyclopedia’s Liquid Density Calculator, water density at 250C =994.72 kg/m3
Using water density, the mass flow rate is converted to volumetric flow rate.
Volumetric flow = 200,000 / 994.72 = 201.06 m3/hr
Also the differential pressure is determined using differential head as,
ΔP = ρgΔh = 994.72 × 9.81 × 30/105 = 2.93 bar
Step2: The next step is to calculate the theoretical pump power requirement. As per the equation, power requirement is the product of volumetric flow (Q) and differential pressure (ΔP).
Power requirement = Q × ΔP = 201.06/3600 m3/s × 2.93 × 105 N/m2
Theoretical power requirement = 16350 Watt = 16.35 kW
Step3: Pump shaft power requirement = Theoretical power requirement / pump efficiency.
For a pump that has been already purchased or has been ordered for manufacturing, the efficiency can be determined using the pump performance curves provided by pump manufacturer. Here the problem statement has specified pump efficiency to be 70%.
Hence, pump shaft power requirement = 16.35 kW / 0.7 = 23.36 kW
Similarly, motor power requirement = Pump shaft power requirement / motor efficiency
Similar to pump efficiency, electric motor efficiency for motors already purchased or ordered, can be provided by the manufacturer of motor. However for purpose of this sample problem the efficiency is to be taken as 90% as per problem statement.
Motor power requirement = 23.36 / 0.9 = 25.95 kW = 25.95 × 1.3596 HP = 35.28 HP
Electric motors are available for following standard Horsepower ratings.
| 1 | 1.5 | 2 | 3 | 5 | 7.5 | 10 | 15 | 20 | 25 | 30 | 40 | 50 |
| 60 | 75 | 100 | 125 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | 600 |
| 700 | 800 | 900 | 1000 | 1250 | 1500 | 1750 | 2000 | 2250 | 2500 | 3000 | 3500 | 4000 |
Hence in order to have satisfy the minimum power requirement, the motor to be purchased has to have power rating of 40 HP or higher.
Check EnggCyclopedia’s pump sizing calculator to easily calculate power requirement of pump. Check this pump sizing calculation with sample problem.
Also check pump affinity laws to understand relation between pump power and speed of shaft as well as diameter of the impeller.