Insulation thickness for pipes is an essential factor in maintaining the desired temperature of fluids flowing through them, while also reducing energy costs. Insulation helps to minimize heat transfer through the pipe and maintain the temperature of the fluid inside it. The thickness of insulation needed for a particular application depends on various factors, such as the temperature of the fluid, the temperature of the surrounding environment, the diameter and length of the pipe, and the insulation material's thermal conductivity.
Table of content:
Heat transfer through pipes
Insulation thickness
Insulation thickness calculation
Critical thickness of insulation
Heat transfer through pipes
Heat transfer is the movement of thermal energy from one object or substance to another due to a temperature difference between them.
In this case, the fluid inside the pipe loses heat to the surrounding atmosphere if its temperature is higher than the temperature of the surrounding air. This occurs through a process known as convection, where heat is transferred through the movement of fluids or gases. The warmer fluid inside the pipe transfers its heat energy to the cooler surrounding air, causing the fluid to cool down.
On the other hand, if the temperature of the pipe is lower than the temperature of the surrounding air, the pipe will gain heat from the environment. This process is also through convection, where the warmer air surrounding the pipe transfers its heat energy to the cooler pipe.
Insulation thickness
Since pipes are often made of materials like steel, copper, or other metals that are good conductors of heat, the heat loss through the pipe can be substantial and can lead to high energy costs. Therefore, it is essential to provide a cover or insulation made of a material that is a poor conductor of heat, such as mineral wool or hemp. This insulation layer will help to minimize the heat loss from the fluid flowing through the pipe and ensure that it maintains its desired temperature, which can be critical in many industrial applications.
The thickness of insulation needed for a particular application depends on various factors, such as the temperature of the fluid inside the pipe, the temperature of the surrounding environment, the diameter and length of the pipe, and the insulation material's thermal conductivity.
The primary purpose of insulation is to reduce heat transfer through the pipe, which is determined by the thermal conductivity of the insulation material. Therefore, the thicker the insulation, the lower the heat transfer rate and the greater the energy savings. However, increasing insulation thickness also adds cost to the project, so it is essential to strike a balance between the cost of insulation and the potential energy savings.
In general, industry standards and guidelines provide recommended insulation thicknesses for different types of piping systems based on their operating conditions.
Insulation thickness calculation
Sample Problem Statement
Calculate insulation thickness (minimum value) required for a pipe carrying steam at 1800C. The pipe size is 8" and the maximum allowable temperature of outer wall of insulation is 500C. Thermal conductivity of the insulation material for the temperature range of the pipe can be taken as 0.04 W/m·K. The heat loss from steam per meter of pipe length has to be limited to 80 W/m.
Solution
Solution to this sample problem is quite straightforward as demonstrated below.
As per EnggCyclopedia's heat conduction article,
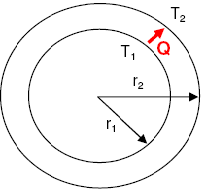
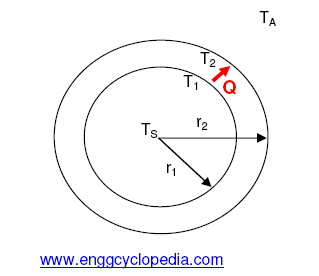
For radial heat transfer by conduction across a cylindrical wall, the heat transfer rate is expressed by following equation,
For the given sample problem,
T1 = Temperature of inner pipe wall = 500C
T2 = Temperature of outer pipe wall = 1800C
r1 = Inner pipe radius = 8" = 8 × 0.0254 m = 0.2032 m
k = Thermal conductivity = 0.04 W/m·K
N = length of the cylinder
Heat loss per unit length of pipe can be calculated as given below.
Q/N = Heat loss per unit length of pipe
Q/N = 80 W/m
Hence, inserting the given numbers in the radial heat transfer rate equation from above,
80 = 2π × 0.04 × (180-50) ÷ ln(r2/0.2032)
ln(r2/0.2032) = 2π × 0.04 × (180-50) / 80 = 0.4084
Hence, r2 = r1 × e0.4084
r2 = 0.2032 × 1.5044 = 0.3057 m
Hence, insulation thickness = r2 - r1
thickness = 305.7 - 203.2 = 102.5 mm
Some margin should be taken to calculate insulation thickness, because if the conductive heat transfer rate happens to be higher than the convective heat transfer rate outside the insulation wall, the outer insulation wall temperature will shoot up to higher values than 500C. Hence conductive heat transfer rate should be limited to lower values than estimates used in this sample problem. The purpose of this sample problem is to demonstrate radial heat conduction calculations and practical calculations of insulation thickness also require consideration of convective heat transfer on the outside of insulation wall.
Critical thickness of insulation
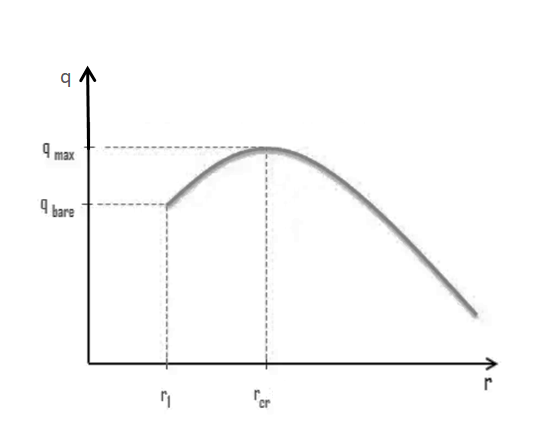
When we add insulation to a plane wall, the heat transfer rate always decreases because the outer surface area remains constant. However, in cylinders and spheres, adding insulation can increase the outer surface area, which decreases the convection resistance at the outer surface. In some cases, this decrease in convection resistance can be more significant than an increase in conduction resistance due to thicker insulation. As a result, the total resistance may actually decrease, resulting in increased heat flow.
The thickness up to which heat flow increases and after which heat flow decreases is termed critical thickness. The critical thickness is the point at which heat flow reaches its maximum and then begins to decrease. For cylinders and spheres, the critical thickness is called the critical radius. We can calculate the critical radius of insulation by considering the thermal conductivity of the insulation material (k) and the external convection heat transfer coefficient (h).
As it can be seen from graph, the total resistance decreases and the heat rate increases as the thickness of the insulation material increases because the outer radius of the insulation is less than the critical radius. However, when the outer radius of the insulation material reaches the critical radius, the heat rate reaches its maximum value. Beyond this point, adding more insulation material would increase the total resistance and decrease heat loss.
Critical thickness of insulation for cylinders can be calculated by,
rcr = k/h
Where, k = Thermal conductivity of material
h = Convective heat transfer coefficient
Critical thickness of insulation for spheres can be calculated by,
rcr = 2k/h
Calculation of critical thickness for a pipe
Assume a steel pipe of r1 = 20 mm, exposed to natural convection at h = 60 W/m2 K. This pipe is insulated by the material of thermal conductivity k = 0.6 W/m K. Determine the critical radius of insulation.
Critical thickness of insulation for a pipe can be calculated by formula rcr = k/h.
rcr = 0.6/60 = 0.01 m
Hence rcr > r1 and heat transfer will increase with the addition of insulation up to a thickness of rcr – r1 = (0.020 – 0.005)m = 0.015 m.