Heat transfer coefficients are a measure of the rate at which heat is transferred between a fluid and a solid surface. It is the proportionality constant between the heat flux and driving force for the heat transfer which is a temperature difference. Check sample problems to understand the calculation of the heat transfer coefficient in various cases.
Table of content:
Calculation of convective heat transfer coefficient
Calculation of overall heat transfer coefficient
Calculation of convective heat transfer coefficient
Problem statement:
Calculate the convective heat transfer coefficient for flow of water at an average bulk temperature of 85oF through a 2 inch diameter pipe that is at 120oF using the Dittus- Boelter equation and using Sieder – Tate equation. The average velocity of water in the pipe is 1.8 ft/sec.
Solution:
Step1: Values for the density, viscosity, specific heat, and thermal conductivity of water a needed at the fluid bulk temperature (85°F) and the viscosity is also needed at the wall temperature (120°F).
Using EnggCyclopedia’s Liquid Density Calculator, density for water at 85°F = 1.93 slugs/ft³
Using EnggCyclopedia’s Liquid Viscosity Calculator,
Water viscosity = 1.64 x 10-5 lb-sec/ft² (slug/ft-sec), = 0.50904 slug/ft-hr
Specific heat (Cp) = 32.2 Btu/slug-°F
Thermal conductivity = 0.33 Btu/hr-ft-°F
Diameter = 2 inch = 2/12 ft = 0.167 ft
Step2: Calculation of Re and Pr are needed for heat transfer coefficient calculation.
Calculation of the Reynolds number (Re).
Re = DVρ /μ = (0.167)(1.8)(1.93) / (1.64 x 10-5) = 35, 305
Calculation of the Prandtl number (Pr).
Pr = μ *Cp / k = {(0.50904) * (32.2)} / (0.33) = 5.8
Step3: Calculation of Nusselt number and heat transfer coefficient based on different equations.
Dittus-Boelter equation
The Dittus Boelter equation is used to calculate the surface coefficient of heat transfer for fluids in turbulent flow inside clean, round pipes. The Dittus-Boelter correlation may be used for small to moderate temperature differences, with all properties evaluated at an, averaged temperature Tavg.
Calculation of the Nusselt number using Dittus-Boelter equation and Sieder-Tate equation.
Dittus-Boelter equation: Nu = 0.023 Re0.8 * Pr0.4
= 0.023 * (35305)0.8 * (5.8)0.4 = 201
Calculate the heat transfer coefficient, h, from the definition of Nu (Nu = hD/k).
h = (Nu)(k) / D = (201 * 0.33) / (0.167) = 399 Btu/hr-ft2-oF
Sieder-Tate equation
The modified form of the Dittus Boelter equation is called Sieder-Tate equation. When the difference between the surface and the fluid temperatures is large, it may be necessary to account for the viscosity variation with temperature. Therefore a modified form of the Dittus-Boelter equation was proposed by Sieder and Tate (1936).
Calculation of the Nusselt number using Sieder-Tate equation.
Sieder-Tate equation: Nu = 0.023 Re0.81 Pr1/3 (μb / μw)0.14
For this equation, the viscosity of the water at the wall temperature (120°F) is also needed.
μb = 1.64 x 10-5 lb-sec/ft² (slug/ft-sec)
μw = 1.16 x 10-5 lb-sec/ft² (slug/ft-sec)
Thus: Nu = 0.023 (35305)0.8 (5.8)1/3 ((1.64 x 10-5)/(1.16 x 10-5 ))0.14 = 188
Calculate the heat transfer coefficient, h, from the definition of Nu (Nu = hD/k)
h = (Nu)(k)/D = 188*0.33/0.167 = 372 Btu/hr-ft²-°F
Gnielinski correlation
The Dittus-Boelter and Sieder-Tate equations are commonly used and appropriate for the purposes of this article, but they can result in errors as high as 25%. To minimize these errors, more recent and complicated correlations like the Gnielinski correlation can be used. This equation is useful for validating tubes over a broad range of Reynolds numbers, including the transition region.
Gnielinski correlation: Nuo = [(f/8) x (Re-1000) x Pr] / [1+{12.7 x (f/8)0.5 x (Pr2/3 -1)}]
Where, f = Moody’s friction factor = (0.790 ln(Re) – 1.64)-2
f = (0.790 ln(35305) – 1.64)-2 = 0.02273
Substituting all values in Gnielinski correlation gives the value of Nuo = 225
Correction for variation in fluid properties is given by,
NuD = Nuo (μb / μw)n , Where n=0.11 for liquid heating n=0.25 for liquid cooling
NuD = 236 (1.41)0.11 = 245
Calculate the heat transfer coefficient h.
h = (NuD)(k)/D = 245 *0.33/0.167 = 485 Btu/hr-ft²-°F
These correlations are used for calculating heat transfer coefficient in the case of forced convection turbulent flow of a fluid inside a circular tube.
Calculation of overall heat transfer coefficient
Problem statement
Determine the overall heat transfer coefficient 'U' for heat transfer occurring from superheated steam in a steel pipe to atmosphere, with the following conditions.
Pipe nominal size = 8"
pipe schedule = STD
Average steam temperature over the pipe length = 2000C
Ambient air temperature = 220C
heat transfer coefficient on steam side = hS = 0.08 W/0Cm2
heat transfer coefficient on air side = hA = 0.04 W/0Cm2
conductivity 'k' of steel = 60 W/mK (at given temperature range)
Solution
Overall heat transfer coefficient for a heat exchanger is a proportionality constant used to calculate overall heat transfer rate between two bodies, arising from the temperature difference between those two bodies.
The sample problem can be solved by following the steps given here. First an equation is developed to determine the overall heat transfer coefficient for this pipe as a function of the individual heat transfer coefficients on both sides as well as the conductivity and then the overall heat transfer coefficient is calculated using the developed equation.
Step1: Refer to EnggCyclopedia's article about heat transfer coefficients, for relation between heat transfer rate and the individual heat transfer coefficients on inside and outside of the pipe.
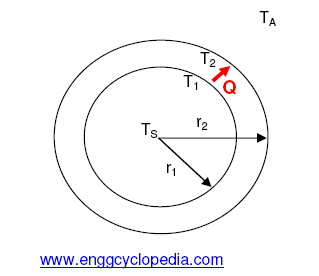
Q = hS×AS×(TS-T1) – steam side heat transfer
(TS-T1) = Q/(hS×AS) ... (1)
Q = hA×AA×(T2-TA) – steam side heat transfer
(TA-T2) = Q/(hA×AA) ... (2)
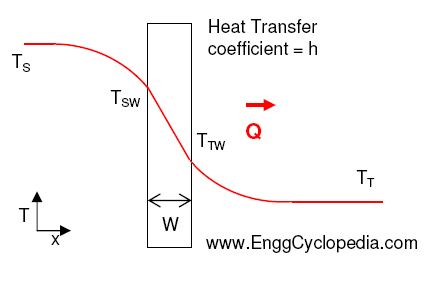
For conductive heat transfer across the pipe wall,
![]()
Hence,
(T1-T2) = Q × ln(r2/r1) / (2πkN) ... (3)
(1) + (2) + (3) gives,
(TS-TA) = (TS-T1) + (TA-T2) + (T1-T2)
(TS-TA) = Q × (1/hS×AS + 1/hA×AA + ln(r2/r1)/2πkN)
Since Q = UA×AA×(TS-TA),
UA = 1/(AA/hSAS + 1/hA + AAln(r2/r1)/2πkN)
Consider unit length of the pipe, i.e. N=1m
Then, AA = 2πr2 and AS = 2πr1
UA = 1/(r2/hSr1 + 1/hA + r2×ln(r2/r1)/k) ... (4)
where N is the tube length and ‘r’ stands for tube radius. The subscripts 1 and 2 stand for inner and outer tube wall respectively. Tube metal conductivity is expressed as ‘k’.
Step2
From EnggCyclopedia's standard piping dimensions calculator, for 8" STD schedule pipe,
pipe inner diameter = d1 = 202.72 mm = 0.20 m
pipe outer diameter = d2 = 219.08 mm = 0.22 m
r10 = 0.1 m and r2 = 0.11 m
Using the given data and equation (4),
UA = 1/(0.11/(0.08×0.10) + 1/0.04 + 0.11×ln(1.1)/60)
UA = 1/(13.75 + 25 + 0.00018) ≈ 1/38.75
UA =0.026 W/0Cm2
Step3
It should be noted that the terms '1/hS', '1/hA' and 'r2×ln(r2/r1)/k' represent the heat transfer resistance for convection inside and outside the pipe and for conduction across the pipe wall, respectively. Smaller magnitude of the heat transfer resistance indicates higher ease of heat transfer.
Thus it can be noted that heat transfer is most easy for conduction across the pipe wall and is represented by a negligible heat transfer resistance value.
On the other hand heat transfer resistance is higher for the convective heat transfer and inversely proportional to the related heat transfer coefficient. Hence it can be seen that most of the heat transfer resistance is contributed by heat transfer on air side of the pipe, which has the lowest heat transfer coefficient.
Finally it can be observed that the overall heat transfer coefficient is lower than heat transfer coefficients on both sides of the pipe. This is explained simply by the definition of the overall heat transfer coefficient which associates it with the largest temperature difference in the heat transfer system.