Heat conduction is the process of transfer of heat energy from one point to another within a solid material or between different materials in physical contact. In this post we will explore a couple of examples of heat conduction calculation - linear heat conduction across a flat wall and radial conduction across the wall of a hollow cylinder.
Table of Content:
1. What is Heat Conduction?
2. Fourier's Law of Heat Conduction
3. Heat Transfer Through a Wall
4. Radial Heat Conduction Through a Hollow Cylinder
What is Heat Conduction?
Conductive heat transfer occurs when heat is transferred through a material without any motion of the material itself. The heat is transferred from molecule to molecule due to lattice vibration and collision of molecules, transferring heat energy from one molecule to the next. This mode of heat transfer takes place in a stagnant medium.
Conduction is the most common mode of heat transfer in solids, and it occurs when there is a temperature gradient within a solid material. The heat flows from regions of high temperature to regions of low temperature to equalize the temperature throughout the material.
The rate of heat transfer through a material by conduction is dependent on the thermal conductivity of the material, the temperature difference across the material, and the area through which heat is being transferred. In general, materials with high thermal conductivity, such as metals, conduct heat more quickly than materials with low thermal conductivity, such as plastics.
Conductive heat transfer can be modeled using equations like Fourier's law of heat conduction.
Fourier's Law of Heat Conduction
Conduction of heat in a solid wall is expressed using Fourier's equation for heat conduction,![]()
T: Temperature at a point in the wall
θ: Time
k: Thermal Conductivity of wall material
A: Cross-sectional area of the element around the point
x: Distance perpendicular to the area element
For steady-state heat transfer, this equation becomes,
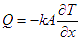
Q: Heat transfer rate
A: Area of the wall
This equation can be further developed to express temperature profiles in various geometries with one-dimensional heat transfer.
Thermal Conductivity Values for Metals
Check this post for the list of thermal conductivity values for metals that can be used for heat transfer calculations around different applications.

Heat Transfer Through a Wall
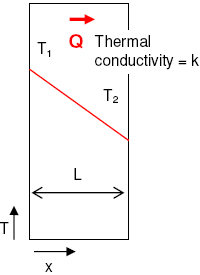
Let's take a case of heat transfer across a flat wall as shown in the figure below.
Assuming that thermal conductivity 'k' is independent of temperature and location and A is independent of location, as is the case for a solid wall with a constant cross-sectional area.
Check below posts for solution of sample problems for different cases of conductive heat transfer though wall.
Conduction across a flat wall
Determine the rate of heat transfer by conduction per unit area, by means of conduction for a furnace wall made of fire clay. Furnace wall thickness is 6" or half a foot. Thermal conductivity of the furnace wall clay is 0.3 W/m·K. The furnace wall temperature can be taken to be same as furnace operating temperature which is 6500C and temperature of the outer wall of the furnace is 1500C.
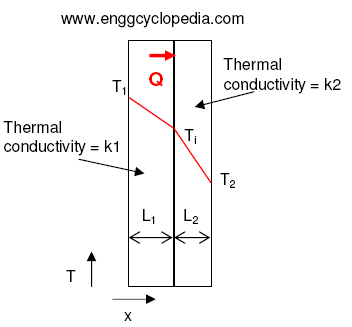
Conduction across a composite wall
Determine the overall heat transfer by conduction per unit area occurring across a furnace wall made of fire clay. Furnace wall has a thickness of 12" or a foot. The wall is insulated from outside. Thermal conductivity values for the wall and insulation materials are 0.1 W/m·K and 0.01 W/m·K, respectively. The furnace operates at 6500C. Average ambient temperature outside the furnace wall is 300C and allowable temperature on the outer side of insulation is 800C. If the air side heat transfer coefficient is 0.4 W/m2·K, calculate the minimum insulation thickness requirement.
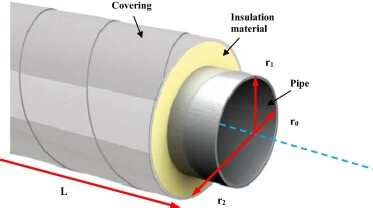
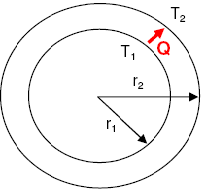
Radial Heat Conduction Through a Hollow Cylinder
Radial heat conduction across the wall of a hollow cylinder is an interesting problem because of the curved geometry of the wall.
Despite the difficulties posed in calculation, this radial heat conduction calculation is quite important in industrial scenarios to determine heat loss (or gain) in a pipe carrying utilities, even in case of shell and tube heat exchangers.
For the radial geometry of a hollow cylinder, the following equation expresses the heat transfer rate.
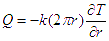
The integral of this equation from inner radius r1 to outer radius r2 represents the total radial heat transfer across the cylindrical wall.
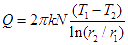
N = length of the hollow cylinder
T1 and T2 are the inner and outer wall temperatures of the hollow cylinder.
Insulation thickness calculation for a pipe
The insulation layer helps to minimize the heat loss from the fluid flowing through the pipe and ensure that it maintains its desired temperature, which can be critical in many industrial applications.
The primary purpose of insulation is to reduce heat transfer through the pipe, which is determined by the thermal conductivity of the insulation material. Therefore, the thicker the insulation, the lower the heat transfer rate and the greater the energy savings. However, increasing insulation thickness also adds cost to the project, so it is essential to strike a balance between the cost of insulation and the potential energy savings.
Check this post for calculation of insulation thickness for a pipe.