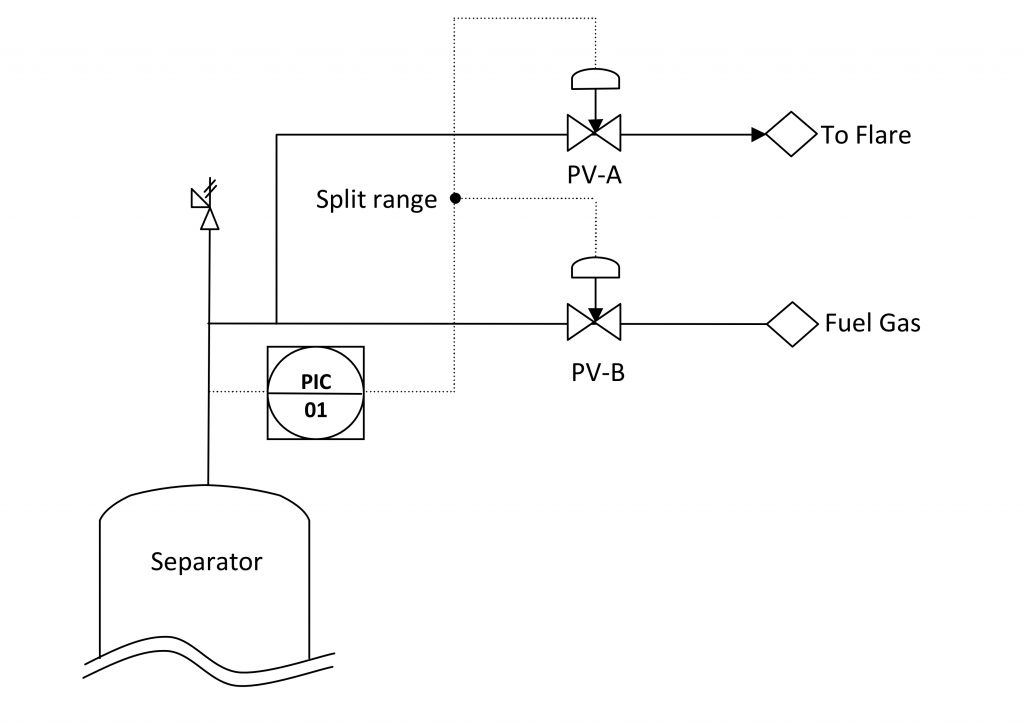
Air being a mixture of gases, does not have a uniformly standard composition. Moreover, density of any gas is subject to the temperature and pressure conditions. Therefore, whenever we speak of air density it is important to also state the temperature and pressure conditions at which the density is calculated.
But often we need a benchmark for air density to be used as reference point in thermodynamic calculations involving air or other gases. For that purpose, we use the concept of "standard air density" which is nothing but air density calculated at standard temperature and pressure conditions.
Now let's look at different sets of standard temperature and pressure conditions and how the air density is calculated at these conditions.
Standard Temperature and Pressure Conditions
Standard air density is density of air calculated at standard temperature and pressure conditions. Standard temperature and pressure (STP) conditions are used as reference points in thermodynamics of gases. Normally standard and normal temperature pressure conditions are used for specifying gas volume. Values of standard temperature and pressure depend on the organization which defines them. Usually the standard pressure is close to atmospheric pressure and standard temperature is close to room temperature value.
Standard Air Density Calculation
The standard density value depends heavily on what definition of standard T & P has been used. Standard conditions as per the IUPAC are:
Standard pressure (P) = 100 kPa
Standard temperature (T) = 0 0C
Let's see how to calculate the air density at these conditions.
Air Molecular weight (MW) = 28.85 gm/mol
Universal gas constant = 8.314 J/K·mol
Air density is then calculated using the formula for density of an ideal gas -
ρ = P×MW/(R×T) = 100×1000×(28.85/1000)/(8.413×(273.16+0))
ρ = 1.2554 kg/m3
However, note that we have used an important approximation here. We have use the ideal gas equation to arrive at "ρ = P×MW/(R×T)". If we consider the same equation for real gas, we need to use the compressibility or Z factor to change it to "ρ = P×MW/(Z×R×T). You can check here for the detailed derivation of this equation and a short tutorial for calculation of gas density.
Alternatively, air density calculator can be used to calculate the air density at these standard temperature and pressure conditions. As per the air density calculator,
ρ = 1.2763 kg/m3
This value matches closely with our calculation for air as an ideal gas at standard temperature and pressure conditions.
You can also use this tutorial as a guideline for calculation for air density
Standard air density values
But that value corresponds to a specific STP conditions specified by IUPAC. Other organizations have defined slightly different standard T & P conditions.
Air density at these different STP conditions is tabulated below.
| Defining Organization | Std Temperature in 0C | Std Pressure in kPa | Standard Air Density in kg/m3 |
| IUPAC | 0 | 100.0 | 1.2554 |
| NIST, ISO 10780 | 0 | 101.325 | 1.2720 |
| ISA, ISO 13443 | 15 | 101.325 | 1.2058 |
| EPA | 25 | 101.325 | 1.1654 |
| SATP | 25 | 100.0 | 1.1501 |
| CAG | 20 | 100.0 | 1.1697 |
| SPE | 15 | 100.0 | 1.1900 |
| ISO 5011 | 20 | 101.3 | 1.1849 |
Geographic variations in air density
Air being a gas, it's density varies as per the temperature and pressure conditions, governed roughly by the ideal gas density equation -
ρ = P×MW/(R×T)
As temperature drops, air density increases. If we move away from hotter tropical regions towards colder, temperate weather air gets denser. However the change is too insignificant to be noticed.
On the other hand air density is directly proportional to pressure. It decreases with decrease in pressure. We can experience significant decrease in air density as we go to higher altitudes and the air pressure drops significantly.
High altitude mountains are well known for problems caused by thin air and lower oxygen levels.
Using the standard density
- The standard density for any gas is is an indicator of the composition of the gas. Density of any gas varies widely with temperature and pressure conditions. Hence the standard temperature and pressure conditions are used as the common reference point at which density can be calculated and compared with other gas mixtures also at STP (standard T & P) conditions.
- In case of air, the standard density value is an indicator of humidity in the air. Moisture content present in the air increases its density and makes it heavier.
- Further, you can also use the standard density value for a variety of engineering calculations involving air or vapor streams. Often, it is easier to convert a gas flow to standard conditions for the purpose of engineering calculations.