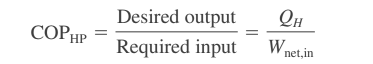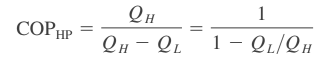A heat pump is a device that transfers heat from a lower-temperature source to a higher-temperature sink by using external energy. Heat pumps are used for both heating and cooling purposes, and they work on the principle of the Second Law of Thermodynamics. The coefficient of performance of a heat pump is an important metric to consider when evaluating the performance of heat pumps.
Table of content:
The second law of thermodynamics
Working of a heat pump
Coefficient of performance of heat pump
The second law of thermodynamics
As heat pump works on the principle of the second law of thermodynamics, it is very important to learn about the second law of thermodynamics.
The second law of thermodynamics is a fundamental principle of nature that governs the behavior of energy and entropy in physical systems. It states that in any natural process, the total entropy of a closed system always increases or remains constant, but never decreases.
Entropy is a measure of the degree of disorder or randomness in a system. According to the second law of thermodynamics, energy tends to flow spontaneously from hot objects to cold objects, and this flow of energy is accompanied by an increase in the entropy of the system. This means that it is impossible to convert heat completely into work without any loss of energy.
There are several statements of the second law of thermodynamics, including the Clausius statement and the Kelvin-Planck statement.
- The Clausius statement states that heat cannot flow spontaneously from a cold object to a hot object without the input of external work.
- The Kelvin-Planck statement states that it is impossible to construct a device that operates in a continuous cycle and produces no effect other than the transfer of heat from a hot object to a cold object.
Working of a heat pump
Before understanding coefficient of performance we must understand working mechanism of heat pump and use of second law of thermodynamics in working of heat pumps.
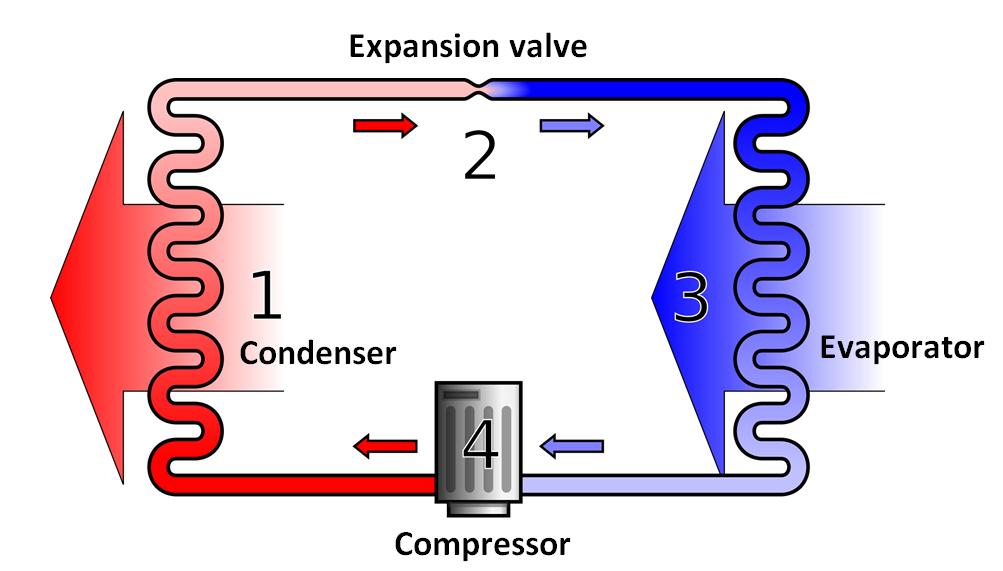
Heat pumps work by transferring heat from a low-temperature source to a high-temperature sink, using the principles of thermodynamics. The refrigeration cycle is the key mechanism that enables this transfer of heat.
- It begins with a low-pressure, low-temperature refrigerant gas that is compressed by a compressor. The compression causes the temperature and pressure of the refrigerant to increase, turning it into a high-pressure, high-temperature gas.
- This hot gas then flows through a heat exchanger, which transfers the heat to the high-temperature sink.
- After the heat is transferred, the refrigerant flows through an expansion valve, which reduces the pressure and temperature of the refrigerant, causing it to evaporate into a low-pressure, low-temperature gas.
- This cold gas then flows through another heat exchanger, which absorbs heat from the low-temperature source, before it returns to the compressor to start the cycle again.
Coefficient of performance of heat pump
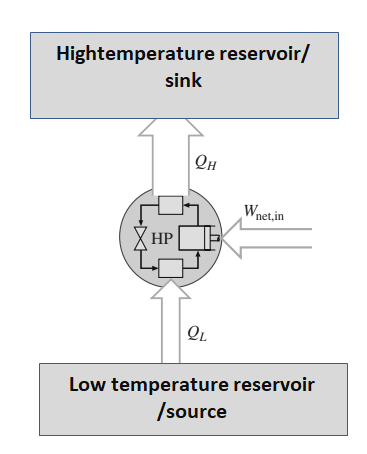
The Coefficient of Performance (COP) is a measure of the efficiency of a heat pump, and it is defined as the ratio of the amount of heat that is transferred to the high-temperature reservoir (the heat output) to the amount of work that is required to transfer the heat (the work input).
For example, if a heat pump requires 1 unit of work to transfer 3 units of heat from a low-temperature source to a high-temperature sink, its COP would be 3:1 or 3.0. A higher COP indicates a more efficient heat pump.
Formula for COP of heat pump is,
Where, QH = Desired heat output to high temperature sink
Wnet,in = Required work input
Where, QL = Heat taken from low temperature source
For fixed values of QL and QH,
Where, COPHP = Coefficient of performance of heat pump
COPR = Coefficient of performance of refrigerator
This relation implies that the coefficient of performance of a heat pump is always greater than unity since COPR is a positive quantity. That is, a heat pump will function, at worst, as a resistance heater, supplying as much energy to the high temperature sink as it consumes. In reality, however, part of QH is lost to the outside air through piping and other devices, and COPHP may drop below unity when the outside air temperature is too low.
In general, the COP of a heat pump is higher when the temperature difference between the high-temperature and low-temperature reservoirs is smaller. This is because it requires less work to transfer heat over a smaller temperature difference. The COP of a heat pump is also influenced by the efficiency of the compressor, which can vary depending on the type and design of the compressor used.
The COP of a heat pump is influenced by a variety of factors, including the temperature difference between the high-temperature and low-temperature reservoirs, the efficiency of the compressor, and the properties of the refrigerant used in the system.