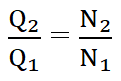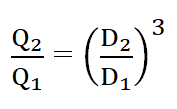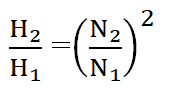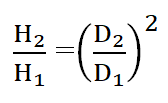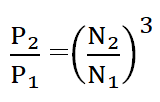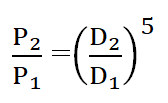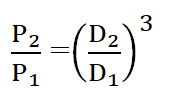Pump affinity laws are a set of mathematical relationships that describe how changes in shaft speed, impeller diameter, or specific gravity affect the flow rate, head, and power requirements of a centrifugal pump. These laws are important because they allow engineers and operators to predict the performance of a pump at different operating conditions, and to optimize its efficiency and reliability.
By applying the pump affinity laws, it is possible to calculate the expected flow rate, head, and power consumption of a pump at a different speed or impeller diameter, without having to conduct expensive and time-consuming experiments.
Table of content:
What are pump affinity laws?
Centrifugal pump affinity laws
Use of affinity laws
What are pump affinity laws?
The pump affinity laws are based on the principle of similarity, which states that if two pumps are geometrically similar, they will exhibit similar performance characteristics when operating under similar conditions.
For example, if we increase the shaft speed of a pump, the flow rate and head will also increase, but the power required to run the pump will increase more rapidly. Similarly, if we increase the impeller diameter, the flow rate and head will increase, but the power required will increase even more. These relationships are described by the pump affinity laws.
The pump affinity laws provide a simple and powerful tool for understanding how centrifugal pumps work, and how we can use them to meet our fluid handling needs.
Centrifugal pump affinity laws
Here's a brief explanation of each law and how it relates to changes in pump speed, impeller diameter.
1. Flow rate
This law states that the flow rate of a centrifugal pump is directly proportional to its speed of the shaft. In other words, if we increase the shaft speed, the flow rate will also increase proportionally.
Mathematically, the relationship of flow rate and shaft speed when diameter is constant can be expressed as:
Where, Q = flow rate and
N = shaft speed of the pump
The flow rate and diameter relation according to power law when the speed of the pump is constant can be expressed as,
D = diameter of the impeller
The relationship will change when the shaft speed (N) is held constant and small variations in impeller diameter are made via trimming. Trimming refers to the process of adjusting the diameter of the impeller by removing material from the impeller vanes. This allows for small changes in the flow rate and head of the pump without changing the speed of the pump.
The flow of the pump (Pump Capacity) is directly proportional to the change in the impeller diameter of the pump. This means there will be the same amount of change in the flow of the pump as the impeller diameter of the pump is changed.
2. Head
This law states that the head, or pressure, developed by a centrifugal pump is proportional to the square of its speed of shaft. This means that if we increase the shaft speed, the head will increase by a factor equal to the square of the speed increase.
Mathematically, the relationship of head and speed of the pump when diameter is constant can be expressed as:
Where, H = Head of the pump
N = shaft speed of the pump
The Head of the pump is proportional to the square of the impeller diameter. This means a change in the pump impeller diameter will lead to a change in the square root of the pump head. In this case relation will remain same for normal and trimmed impeller diameter.
Head and diameter relation according to power law when the speed of the pump is constant can be expressed as,
3. Power
This law states that the power required to operate a centrifugal pump is proportional to the cube of its shaft speed. This means that if we increase the shaft speed of a pump, the power required will increase by a factor equal to the cube of the speed increase.
Mathematically, the affinity law relating the power required and speed of the pump keeping the diameter constant can be expressed as:
Where, P = Power required to operate a pump
N = shaft speed of the pump
Power is proportional to the cube of the impeller diameter. So, when the diameter of the pump is increased the power consumption of the pump will be increased by 8 times.
When speed of the pump is constant, relation between power required and diameter of the pump can be expressed as,
D = diameter of the impeller
We can use the following equation to predict the effect of impeller trimming on pump performance.
It is important to note that the pump affinity laws for impeller trimming are only applicable for small variations in impeller diameter. If the impeller diameter is changed significantly, the performance of the pump may be affected in ways that cannot be predicted by the pump affinity laws alone. In such cases, it may be necessary to perform additional testing or analysis to determine the new performance characteristics of the pump.
In addition to the effects of changes in speed, the pump affinity laws also describe how changes in specific gravity affect pump performance. For example, changing the specific gravity of the fluid being pumped will affect the head and power requirements of the pump.
Use of affinity laws
Pump affinity laws are essential in predicting the performance of a pump under different operating conditions and optimizing pump performance. Here are some practical examples of how the pump affinity laws can be used:
- Predicting pump performance: By using the affinity laws, the performance of a pump can be predicted when the impeller diameter, flow rate, head, or power changes. For instance, if the diameter of the impeller is reduced by 10%, the flow rate will also decrease by 10%, and the head will decrease by 19%. Similarly, if the flow rate is increased by 20%, the power requirement will increase by 73%.
- Optimizing pump performance: The affinity laws can be used to optimize the performance of a pump. For instance, if the pump is operating at a low efficiency, it can be improved by trimming the impeller diameter to increase the head and flow rate. The power consumption can also be reduced by trimming the impeller diameter. Moreover, the affinity laws can be used to select the appropriate pump for a particular application by matching the pump performance with the system requirements.
- Troubleshooting pump performance issues: The affinity laws can be used to troubleshoot pump performance issues. For example, if the flow rate of the pump is not meeting the system requirements, the impeller diameter can be increased to increase the flow rate. Similarly, if the head is not sufficient, the impeller diameter can be decreased to increase the head.
In summary, the pump affinity laws are useful in predicting pump performance, optimizing pump efficiency, selecting the appropriate pump for a specific application, and troubleshooting pump performance issues.