Conduction across a composite wall occurs when heat flows through a wall composed of two or more layers of different materials. The rate of heat transfer by conduction across a composite wall depends on the thermal conductivity, thickness, and surface area of each layer, as well as the temperature difference across the wall. To calculate the rate of heat transfer by conduction across a composite wall, we can use the principle of thermal resistance.
Table of content:
Heat transfer through a wall
Heat transfer through a composite wall
How to calculate rate of heat transfer across a composite wall?
Heat transfer through a wall
Heat transfer through a wall can occur by three modes: conduction, convection, and radiation. Conduction is the transfer of heat through a material without any net motion of the material itself, as described in the previous answer. Convection is the transfer of heat by the motion of a fluid, such as air or liquid, and radiation is the transfer of heat through electromagnetic waves.
When considering heat transfer through a wall, the mode of transfer that dominates depends on the specific circumstances. For example, in a furnace, heat transfer through the furnace wall occurs primarily by conduction since the solid wall material is the primary barrier between the high-temperature furnace interior and the surrounding cooler environment. In a building, heat transfer through the walls can occur by all three modes, but conduction is typically the most significant.
The rate of heat transfer through a wall depends on the thermal conductivity of the wall material, the thickness of the wall, the temperature difference across the wall, and the surface area of the wall.
Heat transfer through a composite wall
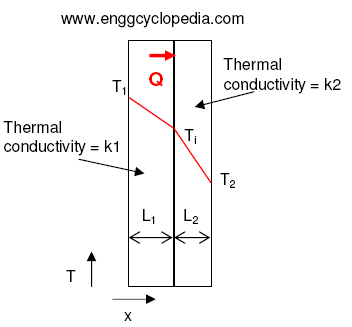
A composite wall consists of two or more layers of different materials with varying thermal conductivities, thicknesses, and boundary conditions. Conduction across a composite wall occurs when heat flows from one side of the wall to the other through multiple layers of different materials. The heat transfer rate through a composite wall depends on the thermal conductivity, thickness, and surface area of each layer, as well as the temperature difference across the wall.
The overall heat transfer rate through a composite wall can be determined by applying the principles of thermal resistance. Each layer of the wall offers a certain amount of thermal resistance to heat flow, and the overall thermal resistance of the composite wall is the sum of the thermal resistances of each layer. This can be expressed mathematically using the equation:
RTotal = R1 + R2 + R3 +... + Rn
Where, RTotal is the total thermal resistance of the composite wall, and R1, R2, R3,...Rn are the thermal resistances of each layer.
The overall heat transfer rate, or heat flux, can then be determined using Fourier's law of heat conduction, which states that the heat flux is proportional to the temperature difference across the wall and inversely proportional to the total thermal resistance of the wall.
Heat transfer through a composite wall can be optimized by selecting materials with high thermal conductivity for the layers with the largest temperature difference, and with low thermal conductivity for the layers with the smallest temperature difference. Additionally, the thickness and surface area of each layer can be adjusted to maximize the overall heat transfer rate.
How to calculate rate of heat transfer across a composite wall?
Problem Statement
Determine the overall heat transfer by conduction per unit area occurring across a furnace wall made of fire clay. Furnace wall has a thickness of 12" or a foot. The wall is insulated from outside. Thermal conductivity values for the wall and insulation materials are 0.1 W/m·K and 0.01 W/m·K, respectively. The furnace operates at 6500C. Average ambient temperature outside the furnace wall is 300C and allowable temperature on the outer side of insulation is 800C. If the air side heat transfer coefficient is 0.4 W/m2·K, calculate the minimum insulation thickness requirement.
Solution
The sample problem can be solved by following the steps given here. First the maximum possible heat transfer rate from furnace wall to the atmosphere is calculated. Then based on this maximum possible rate, minimum requirement of insulation thickness can be estimated.
Step1
Refer to EnggCyclopedia's article about heat transfer coefficients, for relation between heat transfer rate and the individual heat transfer coefficients between wall and air.
Q/A = hA×(T2-TA) – Air side heat transfer rate in W/m2
Hence, Q/A = 0.4×(80-30) = 20.0 W/m2
This is the maximum limit of heat transfer rate through the furnace wall and insulation.
Step2
The conductive heat transfer through a flat wall is described in EnggCyclopedia's article on conduction.
For a flat wall,
Q/A = k1×(T1-Ti)/L1 = k2×(Ti-T2)/L2
Hence,
(T1-Ti) = (Q/A)×(L1/k1)... (1)
and (Ti-T2) = (Q/A)×(L2/k2)... (2)
(1) + (2) gives,
(T1-T2) = (Q/A)×(L1/k1 + L2/k2)... (3)
From this equation we can say that for composite walls with layers of different materials, the overall heat transfer rate can be represented as,
(T1-T2) ÷ (Q/A) = (L1/k1 + L2/k2) = heat transfer resistance
The inverse of heat transfer resistance represents conductive heat transfer coefficient, given by,
Conductive heat transfer coefficient =1 / (L1/k1 + L2/k2) = k1k2/(L1k2+L2k1)
Step3
Maximum allowable heat transfer rate represents minimum insulation thickness requirement. Hence, Q/A = 20.0W/m2
So, in equation (3), all the variables are known except for L2. Hence this equation can be solved to determine L2.
The solution to equation (3) is L2 = 0.25 m or 10 inches.
This is the minimum insulation thickness requirement for furnace wall.
Related reading
- Surface area available for heat transfer is quite an important determinant of the overall heat transfer rate. Understand the importance of this factor with a small thought experiment.